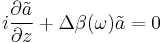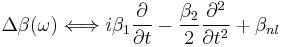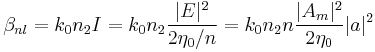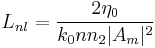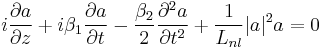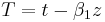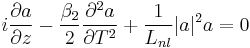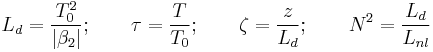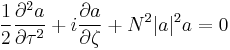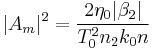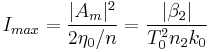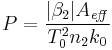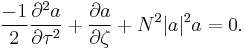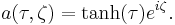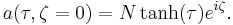Soliton (optics)
In optics, the term soliton is used to refer to any optical field that does not change during propagation because of a delicate balance between nonlinear and linear effects in the medium. There are two main kinds of solitons:
- spatial solitons: the nonlinear effect can balance the diffraction. The electromagnetic field can change the refractive index of the medium while propagating, thus creating a structure similar to a graded-index fiber. If the field is also a propagating mode of the guide it has created, then it will remain confined and it will propagate without changing its shape
- temporal solitons: if the electromagnetic field is already spatially confined, it is possible to send pulses that will not change their shape because the nonlinear effects will balance the dispersion. Those solitons were discovered first and they are often simply referred as "solitons" in optics.
Contents |
Spatial solitons
In order to understand how a spatial soliton can exist, we have to make some considerations about a simple convex lens. As shown in the picture on the right, an optical field approaches the lens and then it is focused. The effect of the lens is to introduce a non-uniform phase change that causes focusing. This phase change is a function of the space and can be represented with 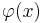 , whose shape is approximately represented in the picture.
, whose shape is approximately represented in the picture.
The phase change can be expressed as the product of the phase constant and the width of the path the field has covered. We can write it as:
where 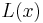 is the width of the lens, changing in each point with a shape that is the same of
is the width of the lens, changing in each point with a shape that is the same of 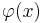 because
because 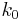 and n are constants. In other words, in order to get a focusing effect we just have to introduce a phase change of such a shape, but we are not obliged to change the width. If we leave the width L fixed in each point, but we change the value of the refractive index
and n are constants. In other words, in order to get a focusing effect we just have to introduce a phase change of such a shape, but we are not obliged to change the width. If we leave the width L fixed in each point, but we change the value of the refractive index 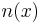 we will get exactly the same effect, but with a completely different approach.
we will get exactly the same effect, but with a completely different approach.
That's the way graded-index fibers work: the change in the refractive index introduces a focusing effect that can balance the natural diffraction of the field. If the two effects balance each other perfectly, then we have a confined field propagating within the fiber.
Spatial solitons are based on the same principle: the Kerr effect introduces a Self-phase modulation that changes the refractive index according to the intensity:
if 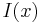 has a shape similar to the one shown in the figure, then we have created the phase behavior we wanted and the field will show a self-focusing effect. In other words, the field creates a fiber-like guiding structure while propagating. If the field creates a fiber and it is the mode of such a fiber at the same time, it means that the focusing nonlinear and diffractive linear effects are perfectly balanced and the field will propagate forever without changing its shape (as long as the medium does not change and if we can neglect losses, obviously). In order to have a self-focusing effect, we must have a positive
has a shape similar to the one shown in the figure, then we have created the phase behavior we wanted and the field will show a self-focusing effect. In other words, the field creates a fiber-like guiding structure while propagating. If the field creates a fiber and it is the mode of such a fiber at the same time, it means that the focusing nonlinear and diffractive linear effects are perfectly balanced and the field will propagate forever without changing its shape (as long as the medium does not change and if we can neglect losses, obviously). In order to have a self-focusing effect, we must have a positive 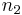 , otherwise we will get the opposite effect and we will not notice any nonlinear behavior.
, otherwise we will get the opposite effect and we will not notice any nonlinear behavior.
The optical waveguide the soliton creates while propagating is not only a mathematical model, but it actually exists and can be used to guide other waves at different frequencies. This way it is possible to let light interact with light at different frequencies (this is impossible in linear media)
Proof
An electric field is propagating in a medium showing optical Kerr effect, so the refractive index is given by:
we remember that the relationship between intensity and electric field is (in the complex representation):
where 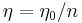 and
and 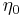 is the impedance of free space, given by:
is the impedance of free space, given by:
The field is propagating in the 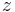 direction with a phase constant
direction with a phase constant 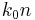 . About now, we will ignore any dependence on the y axis, assuming that it is infinite in that direction. Then the field can be expressed as:
. About now, we will ignore any dependence on the y axis, assuming that it is infinite in that direction. Then the field can be expressed as:
where 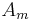 is the maximum amplitude of the field and
is the maximum amplitude of the field and 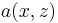 is a dimensionless normalized function (so that its maximum value is 1) that represents the shape of the electric field among the x axis. In general it depends on z because fields change their shape while propagating. Now we have to solve Helmholtz equation:
is a dimensionless normalized function (so that its maximum value is 1) that represents the shape of the electric field among the x axis. In general it depends on z because fields change their shape while propagating. Now we have to solve Helmholtz equation:
where it was pointed out clearly that the refractive index (thus the phase constant) depend on intensity. If we replace the expression of the electric field in the equation, assuming that the envelope 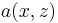 changes slowly while propagating, i.e.
changes slowly while propagating, i.e.
the equation becomes:
Let us introduce an approximation that is valid because the nonlinear effects are always much smaller than the linear ones:
now we express the intensity in terms of the electric field:
the equation becomes:
We will now assume 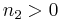 so that the nonlinear effect will cause self focusing. In order to make this evident, we will write in the equation
so that the nonlinear effect will cause self focusing. In order to make this evident, we will write in the equation 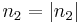 Let us now define some parameters and replace them in the equation:
Let us now define some parameters and replace them in the equation:
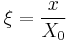 , so we can express the dependence on the x axis with a dimensionless parameter;
, so we can express the dependence on the x axis with a dimensionless parameter; 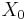 is a length, whose physical meaning will be clearer later.
is a length, whose physical meaning will be clearer later.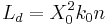 , after the electric field has propagated across z for this length, the linear effects of diffraction can not be neglected anymore.
, after the electric field has propagated across z for this length, the linear effects of diffraction can not be neglected anymore.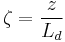 , for studying the z-dependence with a dimensionless variable.
, for studying the z-dependence with a dimensionless variable.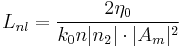 , after the electric field has propagated across z for this length, the nonlinear effects can not be neglected anymore. This parameter depends upon the intensity of the electric field, that's typical for nonlinear parameters.
, after the electric field has propagated across z for this length, the nonlinear effects can not be neglected anymore. This parameter depends upon the intensity of the electric field, that's typical for nonlinear parameters.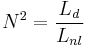
The equation becomes:
this is a common equation known as nonlinear Schrödinger equation. From this form, we can understand the physical meaning of the parameter N:
- if
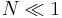 , then we can neglect the nonlinear part of the equation. It means
, then we can neglect the nonlinear part of the equation. It means 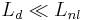 , then the field will be affected by the linear effect (diffraction) much earlier than the nonlinear effect, it will just diffract without any nonlinear behavior.
, then the field will be affected by the linear effect (diffraction) much earlier than the nonlinear effect, it will just diffract without any nonlinear behavior. - if
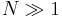 , then the nonlinear effect will be more evident than diffraction and, because of self phase modulation, the field will tend to focus.
, then the nonlinear effect will be more evident than diffraction and, because of self phase modulation, the field will tend to focus. - if
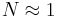 , then the two effects balance each other and we have to solve the equation.
, then the two effects balance each other and we have to solve the equation.
For 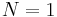 the solution of the equation is simple and it is the fundamental soliton:
the solution of the equation is simple and it is the fundamental soliton:
where sech is the hyperbolic secant. It still depends on z, but only in phase, so the shape of the field will not change during propagation.
For 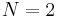 it is still possible to express the solution in a closed form, but it has a more complicated form:
it is still possible to express the solution in a closed form, but it has a more complicated form:
It does change its shape during propagation, but it is a periodic function of z with period 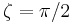 .
.
For soliton solutions, N must be an integer and it is said to be the order or the soliton. For higher values of N, there are no closed form expressions, but the solitons exist and they are all periodic with different periods. Their shape can easily be expressed only immediately after generation:
on the right there is the plot of the second order soliton: at the beginning it has a shape of a sech, then the maximum amplitude increases and then comes back to the sech shape. Since high intensity is necessary to generate solitons, if the field increases its intensity even further the medium could be damaged.
The condition to be solved if we want to generate a fundamental soliton is obtained expressing N in terms of all the known parameters and then putting 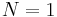 :
:
that, in terms of maximum intensity value becomes:
in most of the cases, the two variables that can be changed are the maximum intensity 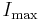 and the pulse width
and the pulse width 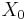 .
.
Generation of Spatial Solitons
The first experiment on spatial optical solitons was reported in 1974 by Ashkin and Bjorkholm[1] in a cell filled with sodium vapor. It was more than another ten years before this field was revisited in experiments at Limoge University[2] in liquid carbon disulphide. After these experiments spatial solitons have been demonstrated in glass, semiconductors[3] and polymers. During the last decade several experiments have been reported on solitons in nematic liquid crystals,[4] also referred to as nematicons.
Temporal solitons
The main problem that limits transmission bit rate in optical fibers is group velocity dispersion. It is because generated impulses have a non-zero bandwidth and the medium they are propagating through has a refractive index that depends on frequency (or wavelength). This effect is represented by the group delay dispersion parameter D; using it, it is possible to calculate exactly how much the pulse will widen:
where L is the length of the fiber and 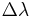 is the bandwidth in terms of wavelength. The approach in modern communication systems is to balance such a dispersion with other fibers having D with different signs in different parts of the fiber: this way the pulses keep on broadening and shrinking while propagating. With temporal solitons it is possible to remove such a problem completely.
is the bandwidth in terms of wavelength. The approach in modern communication systems is to balance such a dispersion with other fibers having D with different signs in different parts of the fiber: this way the pulses keep on broadening and shrinking while propagating. With temporal solitons it is possible to remove such a problem completely.
Consider the picture on the right. On the left there is a standard Gaussian pulse, that's the envelope of the field oscillating at a defined frequency. We assume that the frequency remains perfectly constant during the pulse.
Now we let this pulse propagate through a fiber with 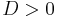 , it will be affected by group velocity dispersion. For this sign of D, the dispersion is anomalous, so that the higher frequency components will propagate a little bit faster than the lower frequencies, thus arriving before at the end of the fiber. The overall signal we get is a wider chirped pulse, shown in the upper right of the picture.
, it will be affected by group velocity dispersion. For this sign of D, the dispersion is anomalous, so that the higher frequency components will propagate a little bit faster than the lower frequencies, thus arriving before at the end of the fiber. The overall signal we get is a wider chirped pulse, shown in the upper right of the picture.
Now let us assume we have a medium that shows only nonlinear Kerr effect but its refractive index does not depend on frequency: such a medium does not exist, but it's worth considering it to understand the different effects.
The phase of the field is given by:
the frequency (according to its definition) is given by:
this situation is represented in the picture on the left. At the beginning of the pulse the frequency is lower, at the end it's higher. After the propagation through our ideal medium, we will get a chirped pulse with no broadening because we have neglected dispersion.
Coming back to the first picture, we see that the two effects introduce a change in frequency in two different opposite directions. It is possible to make a pulse so that the two effects will balance each other. Considering higher frequencies, linear dispersion will tend to let them propagate faster, while nonlinear Kerr effect will slow them down. The overall effect will be that the pulse does not change while propagating: such pulses are called temporal solitons.
History of temporal solitons
In 1973, Akira Hasegawa and Fred Tappert of AT&T Bell Labs were the first to suggest that solitons could exist in optical fibers, due to a balance between self-phase modulation and anomalous dispersion.[5] [6] Also in 1973 Robin Bullough made the first mathematical report of the existence of optical solitons. He also proposed the idea of a soliton-based transmission system to increase performance of optical telecommunications.
Solitons in a fiber optic system are described by the Manakov equations.
In 1987, P. Emplit, J.P. Hamaide, F. Reynaud, C. Froehly and A. Barthelemy, from the Universities of Brussels and Limoges, made the first experimental observation of the propagation of a dark soliton, in an optical fiber.
In 1988, Linn Mollenauer and his team transmitted soliton pulses over 4,000 kilometers using a phenomenon called the Raman effect, named for the Indian scientist Sir C. V. Raman who first described it in the 1920s, to provide optical gain in the fiber.
In 1991, a Bell Labs research team transmitted solitons error-free at 2.5 gigabits over more than 14,000 kilometers, using erbium optical fiber amplifiers (spliced-in segments of optical fiber containing the rare earth element erbium). Pump lasers, coupled to the optical amplifiers, activate the erbium, which energizes the light pulses.
In 1998, Thierry Georges and his team at France Télécom R&D Center, combining optical solitons of different wavelengths (wavelength division multiplexing), demonstrated a data transmission of 1 terabit per second (1,000,000,000,000 units of information per second).
In 2001, the practical use of solitons became a reality when Algety Telecom deployed submarine telecommunications equipment in Europe carrying real traffic using John Scott Russell's solitary wave.
Proof
An electric field is propagating in a medium showing optical Kerr effect through a guiding structure (such as an optical fiber) that limits the power on the xy plane. If the field is propagating towards z with a phase constant 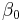 , then it can be expressed in the following form:
, then it can be expressed in the following form:
where 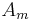 is the maximum amplitude of the field,
is the maximum amplitude of the field, 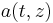 is the envelope that shapes the impulse in the time domain; in general it depends on z because the impulse can change its shape while propagating;
is the envelope that shapes the impulse in the time domain; in general it depends on z because the impulse can change its shape while propagating; 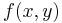 represents the shape of the field on the xy plane, and it does not change during propagation because we have assumed the field is guided. Both a and f are normalized dimensionless functions whose maximum value is 1, so that
represents the shape of the field on the xy plane, and it does not change during propagation because we have assumed the field is guided. Both a and f are normalized dimensionless functions whose maximum value is 1, so that 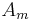 really represents the field amplitude.
really represents the field amplitude.
Since in the medium there is a dispersion we can not neglect, the relationship between the electric field and its polarization is given by a convolution integral. Anyway, using a representation in the Fourier domain, we can replace the convolution with a simple product, thus using standard relationships that are valid in simpler media. We Fourier-transform the electric field using the following definition:
using this definition, a derivative in the time domain corresponds to a product in the Fourier domain:
the complete expression of the field in the frequency domain is:
Now we can solve Helmholtz equation in the frequency domain:
we decide to express the phase constant with the following notation:
where we assume that 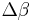 (the sum of the linear dispersive component and the non linear part) is a small perturbation, i.e.
(the sum of the linear dispersive component and the non linear part) is a small perturbation, i.e. 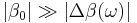 . The phase constant can have any complicated behavior, but we can represent it with a Taylor series centered on
. The phase constant can have any complicated behavior, but we can represent it with a Taylor series centered on 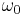 :
:
where, as known:
we put the expression of the electric field in the equation and make some calculations. If we assume the slowly varying envelope approximation:
we get:
we are ignoring the behavior in the xy plane, because it is already known and given by 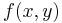 . We make a small approximation, as we did for the spatial soliton:
. We make a small approximation, as we did for the spatial soliton:
replacing this in the equation we get simply:
now we want to come back in the time domain. Expressing the products by derivatives we get the duality:
we can write the non linear component in terms of the amplitude of the field:
for duality with the spatial soliton, we define:
and this symbol has the same meaning of the previous case, even if the context is different. The equation becomes:
We know that the impulse is propagating among the z axis with a group velocity given by 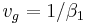 , so we are not interested in it because we just want to know how the pulse changes its shape while propagating. We decide to study the impulse shape, i.e. the envelope function a(.) using a reference that is moving with the field at the same velocity. Thus we make the substitution
, so we are not interested in it because we just want to know how the pulse changes its shape while propagating. We decide to study the impulse shape, i.e. the envelope function a(.) using a reference that is moving with the field at the same velocity. Thus we make the substitution
and the equation becomes:
we assume the medium where the field is propagating to show anomalous dispersion, i.e. 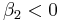 or in term of the group delay dispersion parameter
or in term of the group delay dispersion parameter 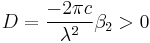 . We make this more evident replacing in the equation
. We make this more evident replacing in the equation 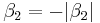 . Let us define now the following parameters (the duality with the previous case is evident):
. Let us define now the following parameters (the duality with the previous case is evident):
replacing those in the equation we get:
that is exactly the same equation we have obtained in the previous case. The first order soliton is given by:
the same considerations we have made are valid in this case. The condition 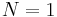 becomes a condition on the amplitude of the electric field:
becomes a condition on the amplitude of the electric field:
or, in terms of intensity:
or we can express it in terms of power if we introduce an effective area 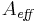 defined so that
defined so that 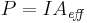 :
:
Stability of solitons
We have described what optical solitons are and, using mathematics, we have seen that, if we want to create them, we have to create a field with a particular shape (just sech for the first order) with a particular power related to the duration of the impulse. But what if we are a bit wrong in creating such impulses? Adding small perturbations to the equations and solving them numerically, it is possible to show that mono-dimensional solitons are stable. They are often referred as (1 + 1) D solitons, meaning that they are limited in one dimension (x or t, as we have seen) and propagate in another one (z).
If we create such a soliton using slightly wrong power or shape, then it will adjust itself until it reaches the standard sech shape with the right power. Unfortunately this is achieved at the expense of some power loss, that can cause problems because it can generate another non-soliton field propagating together with the field we want. Mono-dimensional solitons are very stable: for example, if 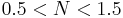 we will generate a first order soliton anyway; if N is greater we'll generate a higher order soliton, but the focusing it does while propagating may cause high power peaks damaging the media.
we will generate a first order soliton anyway; if N is greater we'll generate a higher order soliton, but the focusing it does while propagating may cause high power peaks damaging the media.
The only way to create a (1 + 1) D spatial soliton is to limit the field on the y axis using a dielectric slab, then limiting the field on x using the soliton.
On the other hand, (2 + 1) D spatial solitons are unstable, so any small perturbation (due to noise, for example) can cause the soliton to diffract as a field in a linear medium or to collapse, thus damaging the material. It is possible to create stable (2 + 1) D spatial solitons using saturating nonlinear media, where the Kerr relationship 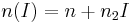 is valid until it reaches a maximum value. Working close to this saturation level makes it possible to create a stable soliton in a three dimensional space.
is valid until it reaches a maximum value. Working close to this saturation level makes it possible to create a stable soliton in a three dimensional space.
If we consider the propagation of shorter (temporal) light pulses or over a longer distance, we need to consider higher-order corrections and therefore the pulse carrier envelope is governed by the higher-order nonlinear Schrödinger equation (HONSE) for which there are some specialized (analytical) soliton solutions.[7]
Effect of power losses
As we have seen, in order to create a soliton it is necessary to have the right power when it is generated. If there are no losses in the medium, then we know that the soliton will keep on propagating forever without changing shape (1st order) or changing its shape periodically (higher orders). Unfortunately any medium introduces losses, so the actual behavior of power will be in the form:
this is a serious problem for temporal solitons propagating in fibers for several kilometers. Let us consider what happens for the temporal soliton, generalization to the spatial ones is immediate. We have proved that the relationship between power 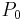 and impulse length
and impulse length 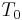 is:
is:
if the power changes, the only thing that can change in the second part of the relationship is 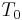 . if we add losses to the power and solve the relationship in terms of
. if we add losses to the power and solve the relationship in terms of 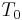 we get:
we get:
the width of the impulse grows exponentially to balance the losses! this relationship is true as long as the soliton exists, i.e. until this perturbation is small, so it must be  otherwise we can not use the equations for solitons and we have to study standard linear dispersion. If we want to create a transmission system using optical fibers and solitons, we have to add optical amplifiers in order to limit the loss of power.
otherwise we can not use the equations for solitons and we have to study standard linear dispersion. If we want to create a transmission system using optical fibers and solitons, we have to add optical amplifiers in order to limit the loss of power.
Generation of soliton pulse
Experiments has been carried out to analyze the effect of high frequency (20 MHz-1 GHz) external magnetic field induced nonlinear Kerr effect on Single mode optical fiber of considerable length (50-100m) to compensate group velocity dispersion (GVD) and subsequent evolution of soliton pulse ( peak energy, narrow, secant hyperbolic pulse).[8] Generation of soliton pulse in fiber is an obvious conclusion as self phase modulation due to high energy of pulse offset GVD, whereas the evolution length is 2000 km. (the laser wavelength chosen greater than 1.3 micrometers). Moreover peak soliton pulse is of period 1-3ps so that it is safely accommodated in the optical bandwidth. Once soliton pulse is generated it is least dispersed over thousands of kilometers length of fiber limiting the number of repeater station.
Dark solitons
In the analysis of both types of solitons we have assumed particular conditions about the medium:
- in spatial solitons,
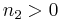 , that means the self-phase modulation causes self-focusing
, that means the self-phase modulation causes self-focusing - in temporal solitons,
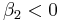 or
or 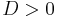 , anomalous dispersion
, anomalous dispersion
Is it possible to obtain solitons if those conditions are not verified? if we assume 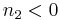 or
or 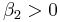 , we get the following differential equation (it has the same form in both cases, we will use only the notation of the temporal soliton):
, we get the following differential equation (it has the same form in both cases, we will use only the notation of the temporal soliton):
This equation has soliton-like solutions. For the first order (N=1):
The plot of 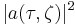 is shown in the picture on the right. For higher order solitons (
is shown in the picture on the right. For higher order solitons (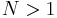 ) we can use the following closed form expression:
) we can use the following closed form expression:
It is a soliton, in the sense that it propagates without changing its shape, but it is not made by a normal pulse; rather, it is a lack of energy in a continuous time beam. The intensity is constant, but for a short time during which it jumps to zero and back again, thus generating a "dark pulse"'. Those solitons can actually be generated introducing short dark pulses in much longer standard pulses. Dark solitons are more difficult to handle than standard solitons, but they have shown to be more stable and robust to losses.
See also
Notes
- ^ J.E. Bjorkholm, A. Ashkin (1974). "cw Self-Focusing and Self-Trapping of Light in Sodium Vapor". Phys. Rev. Lett. 32 (4): 129. Bibcode 1974PhRvL..32..129B. doi:10.1103/PhysRevLett.32.129.
- ^ A. Barthelemy, S. Maneuf and C. Froehly (1985). "Propagation soliton et auto-confinement de faisceaux laser par non linearité optique de kerr". Opt. Comm. 55 (3): 201. Bibcode 1985OptCo..55..201B. doi:10.1016/0030-4018(85)90047-1.
- ^ J.S. Aitchison et al. (1992). "Observation of spatial solitons in AlGaAs waveguides". Electron. Lett. 28 (20): 1879. doi:10.1049/el:19921203.
- ^ J. Beeckman, K. Neyts, X. Hutsebaut, C. Cambournac, M. Haelterman (2004). "Simulations and Experiments on Self-focusing Conditions in Nematic Liquid-crystal Planar Cells". Opt. Express 12 (6): 1011–1018. Bibcode 2004OExpr..12.1011B. doi:10.1364/OPEX.12.001011. PMID 19474916. [1][2]
- ^ ""Solitons in Telecommunications" in the book _Nonlinear Science_ (Chapter 3)". http://www.nap.edu/openbook.php?record_id=5833&page=7.
- ^ ""Making Waves: Solitons and Their Optical Applications" from SIAM News, Volume 31, Number 2". http://www.siam.org/pdf/news/810.pdf.
- ^ M. Gedalin, T.C. Scott, and Y.B. Band, "Optical Solitons in the Higher Order Nonlinear Schrödinger Equation", Phys. Rev. Lett. 78: 448-451 (1997) [3][4].
- ^ S.Chakraborty, "Report of soliton pulse generation within 50 m length of SM fiber by high frequency induced nonlinear intelligent feedback method" , Proceedings, IEEE National Conference on Applications of Intelligent System, Sonepat, India, pp.91–94, 2008, ISBN 978-81-906531-0-7.
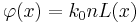
![\varphi (x) = k_0 n (x) L = k_0 L [n %2B n_2 I(x)]](/2012-wikipedia_en_all_nopic_01_2012/I/7dcf6ec80413c5ea66045e3eb2509f4b.png)
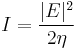
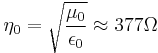
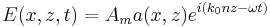
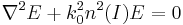
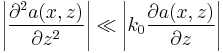
![\frac{\partial^2 a}{\partial x^2} %2B i 2 k_0 n \frac{\partial a}{\partial z} %2B k_0^2 [n^2 (I) - n^2] a = 0](/2012-wikipedia_en_all_nopic_01_2012/I/cc94f0dc02ddbbcdd5c7755cad144622.png)
![[n^2 (I) - n^2] = [n (I) - n] [n (I) %2B n] = n_2 I (2 n %2B n_2 I) \approx 2 n n_2 I](/2012-wikipedia_en_all_nopic_01_2012/I/d3f17d078fe70e997a3a6747b38aa98c.png)
![[n^2 (I) - n^2] \approx 2 n n_2 \frac{|A_m|^2 |a(x,z)|^2 }{2 \eta_0 / n} = n^2 n_2 \frac{|A_m|^2 |a(x,z)|^2 }{\eta_0}](/2012-wikipedia_en_all_nopic_01_2012/I/fad0f0eacabd87563766f9e295c8595a.png)
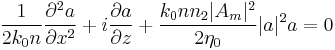
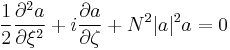

![a(\xi,\zeta) = \frac{4[\cosh (3 \xi) %2B 3 e^{4 i \zeta} \cosh (\xi)] e^{i \zeta / 2}}{\cosh (4 \xi) %2B 4 \cosh (2 \xi) %2B 3 \cos (4 \zeta)}](/2012-wikipedia_en_all_nopic_01_2012/I/663a803e5c0b99d58c8440583762e5f1.png)
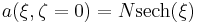
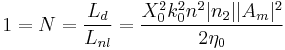
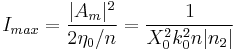
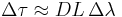
![\varphi (t) = \omega_0 t - k z = \omega_0 t - k_0 z [n %2B n_2 I(t)]](/2012-wikipedia_en_all_nopic_01_2012/I/983ce0f7507e4a325b1be24ee4bf22c7.png)
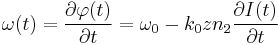
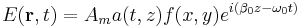
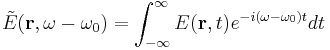
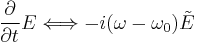
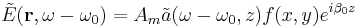
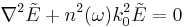
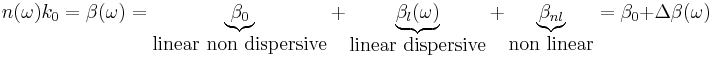
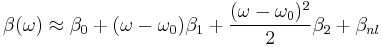
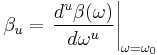
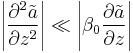
![2 i \beta_0 \frac{\partial \tilde{a}}{\partial z} %2B [\beta^2 (\omega) - \beta_0^2] \tilde{a} = 0](/2012-wikipedia_en_all_nopic_01_2012/I/11ba5fd5cca8b900a2b57954587061be.png)
![\beta^2 (\omega) - \beta_0^2 = [ \beta (\omega) - \beta_0 ] [ \beta (\omega) %2B \beta_0 ] =
[ \beta_0 %2B \Delta \beta (\omega) - \beta_0 ] [2 \beta_0 %2B \Delta \beta (\omega) ] \approx 2 \beta_0 \Delta \beta (\omega)](/2012-wikipedia_en_all_nopic_01_2012/I/577d2a2dd0d82706908355a724b6a0a8.png)